
Figure 1. Kingsbury Radial
and Thrust Pad Bearing
Journal Bearings and Their Lubrication
Journal or plain bearings consist of a shaft or journal which rotates freely in a supporting metal sleeve or shell. There are no rolling elements in these bearings. Their design and construction may be relatively simple, but the theory and operation of these bearings can be complex. This article concentrates on oil- and grease-lubricated full fluid film journal bearings; but first a brief discussion of pins and bushings, dry and semilubricated journal bearings, and tilting-pad bearings.
Low-speed pins and bushings are a form of journal bearing in which the shaft or shell generally does not make a full rotation. The partial rotation at low speed, before typically reversing direction, does not allow for the formation of a full fluid film and thus metal-to-metal contact does occur within the bearing. Pins and bushings continually operate in the boundary lubrication regime. These types of bearings are typically lubricated with an extreme pressure (EP) grease to aid in supporting the load. Solid molybdenum disulfide (moly) is included in the grease to enhance the load-carrying capability of the lubricant. Many outdoor construction and mining equipment applications incorporate pins and bushings. Consequently, shock loading and water and dirt contamination are often major factors in their lubrication.
Dry journal bearings consist of a shaft rotating in a dry sleeve, usually a polymer, which may be blended with solids such as molybdenum, graphite, PTFE or nylon. These bearings are limited to low-load and low-surface speed applications. Semilubricated journal bearings consist of a shaft rotating in a porous metal sleeve of sintered bronze or aluminum in which lubricating oil is contained within the pores of the porous metal. These bearings are restricted to low loads, low-to-medium velocity and temperatures up to 100°C (210°F).
Tilting-pad or pivoting-shoe bearings consist of a shaft rotating within a shell made up of curved pads. Each pad is able to pivot independently and align with the curvature of the shaft. A diagram of a tilt-pad bearing is presented in Figure 1. The advantage of this design is the more accurate alignment of the supporting shell to the rotating shaft and the increase in shaft stability which is obtained.

Figure
1. Kingsbury Radial
and Thrust Pad Bearing
Journal bearings are meant to include sleeve, plain, shell and babbitt bearings. The term babbitt actually refers to the layers of softer metals (lead, tin and copper) which form the metal contact surface of the bearing shell. These softer metals overlay a stronger steel support shell and are needed to cushion the shell from the harder rotating shaft.
Simple shell-type journal bearings accept only radial loading, perpendicular to the shaft, generally due to the downward weight or load of the shaft. Thrust or axial loads, along the axis of the shaft, can also be accommodated by journal bearings designed for this purpose. Figure 1 shows a tilt-pad bearing capable of accepting both radial and thrust loads.
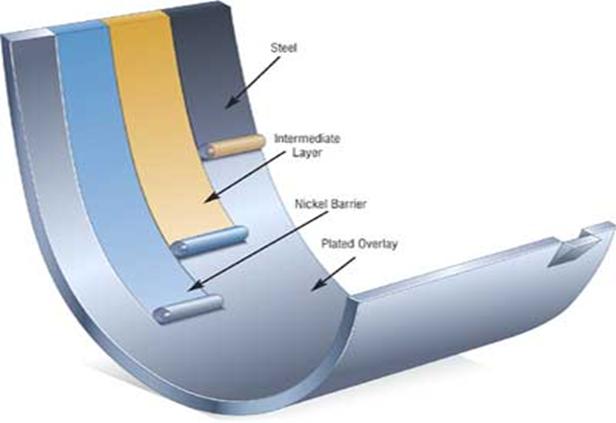
Figure
2. Layers of Journal Bearing Structure
Journal bearings operate in the boundary regime (metal-to-metal contact) only during the startup and shutdown of the equipment when the rotational speed of the shaft (journal) is insufficient to create an oil film. It is during startup and shutdown when almost all of the damage to the bearing occurs. Hydrostatic lift, created by an external pressurized oil feed, may be employed to float large, heavy journals prior to startup (shaft rotation) to prevent this type of damage. During normal operation, the shaft rotates at sufficient speed to force oil between the conforming curved surfaces of the shaft and shell, thus creating an oil wedge and a hydrodynamic oil film. This full hydrodynamic fluid film allows these bearings to support extremely heavy loads and operate at high rotational speeds. Surface speeds of 175 to 250 meters/second (30,000 to 50,000 feet/minute) are common. Temperatures are often limited by the lubricant used, as the lead and tin babbitt is capable of temperatures reaching 150°C (300°F).
It is important to understand that the rotating shaft is not centered in the bearing shell during normal operation. This offset distance is referred to as the eccentricity of the bearing and creates a unique location for the minimum oil film thickness, as illustrated in Figure 3.

Figure
3. Shaft Motion During Startup
Normally, the minimum oil film thickness is also the dynamic operating clearance of the bearing. Knowledge of the oil film thickness or dynamic clearances is also useful in determining filtration and metal surface finish requirements. Typically, minimum oil film thicknesses in the load zone during operation ranges from 1.0 to 300 microns, but values of 5 to 75 microns are more common in midsized industrial equipment. The film thickness will be greater in equipment which has a larger diameter shaft. Persons requiring a more exact value should seek information on the Sommerfeld Number and the Reynolds Number. Discussion of these calculations in greater detail is beyond the scope of this article. Note that these values are significantly larger than the one-micron values encountered in rolling element bearings.
The pressures encountered in the contact area of journal bearings are significantly less than those generated in rolling bearings. This is due to the larger contact area created by the conforming (similar curvature) surfaces of the journal and the shell. The mean pressure in the load zone of a journal bearing is determined by the force per unit area or in this case, the weight or load supported by the bearing divided by the approximate load area of the bearing (the bearing diameter times the length of the bearing). In most industrial applications, these values range from 690 to 2,070 kPa (100 to 300 psi). At these low pressures, there is virtually no increase in the oil viscosity in the bearing contact area due to pressure. Automotive reciprocating engine bearings and some severely loaded industrial applications may have mean pressures of 20.7 to 35 MPa (3,000 to 5,000 psi). At these pressure levels, the viscosity may slightly increase. The maximum pressure encountered by the bearing is typically about twice the mean value, to a maximum of about 70 MPa (10,000 psi).
Oil whirl is a phenomenon that can occur in high-speed journal bearings when the shaft position within the shell becomes unstable and the shaft continues to change its position during normal operation, due to the fluid forces created within the bearing. Oil whirl may be reduced by increasing the load or changing the viscosity, temperature or oil pressure in the bearing. A permanent solution may involve a new bearing with different clearances or design. Oil whip occurs when the oil whirl frequency coincides with the system’s natural frequency. The result can be a catastrophic failure.
Oil
Lubrication
Oils
are used in journal bearings when cooling is required or contaminants
or debris need to be flushed away from the bearing. High-speed
journal bearings are always lubricated with oil rather than a grease.
Oil is supplied to the bearing by either a pressurized oil pump
system, an oil ring or collar or a wick. Grooves in the bearing shell
are used to distribute the oil throughout the bearings’
surfaces.
The viscosity grade required is dependent upon bearing RPM, oil temperature and load. The bearing speed is often measured strictly by the revolutions per minute of the shaft, with no consideration of the surface speed of the shaft, as per the “ndm” values calculated for rolling bearings. Table 1 provides a general guideline to selecting the correct ISO viscosity grade.
The ISO grade number indicated is the preferred grade for speed and temperature range. ISO 68- and 100-grade oils are commonly used in indoor, heated applications, with 32-grade oils being used for high-speed (10,000 RPM) units and some outdoor low-temperature applications.
Note in the table that the higher the bearing speed, the lower the oil viscosity required; and that the higher the operating temperature of the unit, the higher the oil viscosity that is required. If vibration or minor shock loading is possible, a higher grade of oil than the one indicated in Table 1 should be considered.
|
Bearing Speed |
Bearing / Oil Temperature (°C) |
|||
|
(rpm) |
0 to 50 |
60 |
75 |
90 |
|
300 to 1,500 |
- |
68 |
100 to 150 |
- |
|
~1,800 |
32 |
32 to 46 |
68 to 100 |
100 |
|
~3,600 |
32 |
32 |
46 to 68 |
68 to 100 |
|
~10,000 |
32 |
32 |
32 |
32 to 46 |
Table 1. Journal Bearing ISO Viscosity Grade Selection
Another method of determining the proper viscosity grade is by applying minimum and optimum viscosity criteria to a viscosity-temperature plot. A generally accepted minimum viscosity of the oil at the operating temperature for journal bearings is 13 cSt, although some designs allow for an oil as thin as 7 or 8 cSt at the operating temperature. The optimum viscosity at operating temperature is 22 to 35 cSt, for moderate-speed bearings if no shock loading occurs. The optimum viscosity may be as high as 95 cSt for low-speed, heavily loaded or shock-loaded journal bearings.
Using this method requires some knowledge of the oil temperature within the bearing under operating conditions, which can be difficult to determine. Fortunately, an accurate oil temperature is not needed for most viscosity determinations. It is common to determine the temperature of the outer surface of the pipes carrying oil to and away from the bearing. The temperature of the oil inside of the pipes will generally be higher (5 to 10°C, 10 to 18°F) than the outer metal surface of the pipe. The oil temperature within the bearing can be taken as the average of the oil entering versus the temperature exiting the bearing.4
A third and more complex method is to calculate the oil viscosity needed to obtain a satisfactory oil film thickness. Persons wishing to learn more about this method should seek information regarding the Sommerfeld equation and either eccentricity ratios or Reynolds Numbers.4
If the oil selected is too low in viscosity, heat will generate due to an insufficient film thickness and some metal-to-metal contact will occur. If the oil is too high in viscosity, heat will again be generated, but due to the internal fluid friction created within the oil. Selecting an oil which is too high in viscosity can also increase the likelihood of cavitation. The high- and low-pressure zones, which are created within the oil on each side of the area of minimum film thickness, can cause oil cavitation in these bearings. Cavitation is a result of expansion of dissolved air or a vapor (water or fuel) in the low-pressure zone of the bearing. The resulting bubble implodes, causing damage, as it passes through the high-pressure portion of the bearing. If the implosion or collapse of the vapor bubble occurs next to the metal surface, this can cause cavitation pitting damage to the metal. If the implosion of the bubble occurs within the oil, a micro hot spot or micro-dieseling can occur, which may lead to varnishing within the system.
Typically, a rust and oxidation (R&O) inhibited additive system is used in the oils employed in these applications. Antifoam and pour point depressant additives may also be present. Antiwear (AW) hydraulic oils may also be used as long as the high-temperature limit of the zinc AW component is not exceeded and excessive water is not present. R&O oils tend to have better water separation characteristics, which is beneficial, and the AW properties of a hydraulic oil would be beneficial only during startup and shutdown, assuming a properly operating bearing.
Circulating
Oil Systems
Larger
volumes of oil for high-speed machinery are commonly supplied from an
independent reservoir with its associated piping system, cooler and
filters.
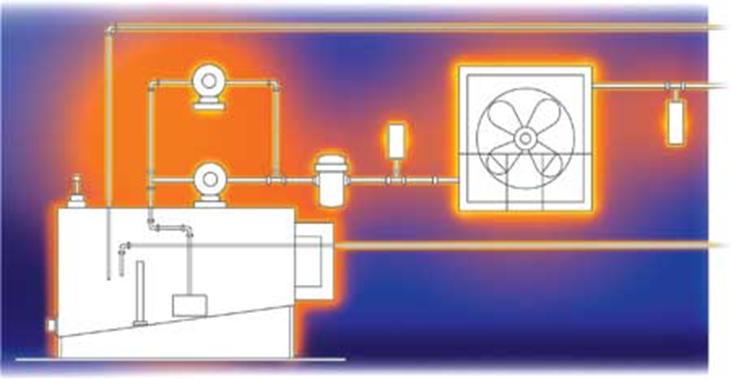
Figure
2. Circulating Oil System Arrangement.
Figure illustrates a typical oil system arrangement with oil from a reservoir being pumped through a filter, cooler, and piping to the lubricated machine components before draining back to the reservoir. Useful information for determining reservoir capacity and pump requirements, filter type and oil dwell time for various applications is summarized in Table 1.
These notes will introduce some of the theory and describe the calculation procedure for an fluid lubricated plain journal bearing design.
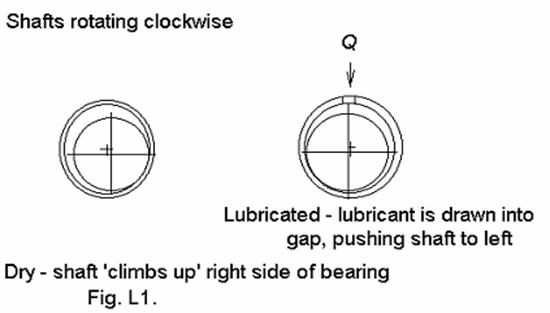
In a dry bearing, the shaft tends to 'climb' up the bearing, whereas in a lubricated bearing, the lubricant being drawn into the bearing tends to push the shaft away from the bearing on the entry side, see Fig.L1.
Newtons Law of Viscous Flow: The shear stress in a fluid is proportional to the rate of change of velocity with respect to 'y', ie:
![]()
where
![]() is
the dynamic or absolute viscosity
is
the dynamic or absolute viscosity
If it is assumed that the shear rate is constant, then: du/dy = U/h and
![]()
Units of absolute viscosity are Pa.s or N.s/m2.
The ASTM method for determining viscosity uses a 'Saybolt Universal Viscometer' and involves measuring the time taken by a volume of fluid to descend a specific distance down a tube of a certain diameter.
Petroff's Law: If a shaft radius, r, is rotating in a bearing, length, l, and radial clearance, c at 'N' revs per s, then the surface velocity is:
![]() m/s
m/s
The shearing stress is the velocity gradient x viscosity:
![]()
The torque to shear the film is force x lever arm length:
![]()
If a small force, w, is applied normal to the shaft axis, the pressure in N/m2 is:
p = w/2rl The frictional force is fw, where f is the coefficient of friction, so the frictional torque is:
T = fwr = (f)(2rlp)(r) = 2r2flp
Equating the two expressions for T and solving for f gives:
![]()
which is Petroff's Law.
![]() and
and
![]() are
dimensionless groups.
are
dimensionless groups.
The bearing characteristic or Sommerfield Number is defined as:
![]()
This is a key quantity in bearing design.
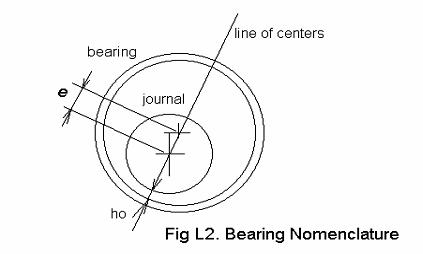
Fig.L2.shows some bearing nomenclature
Assumptions:
1 The lubricant obeys Newton's laws of viscous flow.
2 Intertia effects of the lubricant are neglected.
3 The lubricant is incompressible.
4 The viscosity of the lubricant is constant throughout the film.
5 The pressure does not vary in the axial direction.
6 The curvature of the bearing can be ignored.
7 There is no flow in the axial (z) direction.
8 The film pressure is constant in the 'y' direction, and depends upon 'x'.
· 9 The velocity of a lubricant particle depends on its x and y coordinates.
From the free body diagram of the forces acting on a small cube of lubricant:
![]() and
as
and
as
![]() then
then
![]()
Assuming there is no slip at the boundary, with x held constant, integrate twice with respect to y which gives:
![]() which
is the velocity distribution as a function of y and the
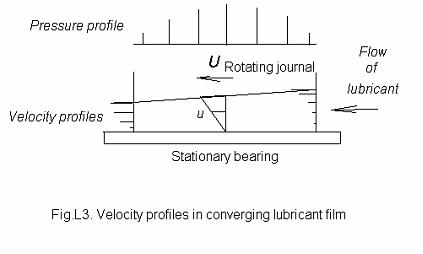
pressure gradient, dp/dx. see Fig.L3. The velocity
distribution accross the film is obtained by superimposing a
parabolic distribution (the first term) onto a linear distribution
(the second term). When the pressure is a maximum, dp/dx = 0
and the velocity is u = - Uy/h.
which
is the velocity distribution as a function of y and the
pressure gradient, dp/dx. see Fig.L3. The velocity
distribution accross the film is obtained by superimposing a
parabolic distribution (the first term) onto a linear distribution
(the second term). When the pressure is a maximum, dp/dx = 0
and the velocity is u = - Uy/h.
If
Q is the quantity of fluid flowing in the x direction per unit
time:
![]() In
practice these integrations have to be modified to include the
effects of end leakage etc.
In
practice these integrations have to be modified to include the
effects of end leakage etc.