Bearing operating principle

The task of a bearing

The task of the bearing is to transform directional motion into rotational motion. This leads to direct contact between the pin and the bearing and causes friction, which in turn causes heat and wear. In order to meet the requirements of operational security, low friction and long lifetime, friction must be reduced by lubrication. The ideal is achieved when the bearing running surface and the pin surface are kept fully separated by a lubricating film. In this case friction amounts to only a fraction of that for direct contact between bearing and pin without lubrication.

However, even this significantly reduced friction generates heat. As long as this heat can be dissipated, the lubricating film is completely maintained and the bearing material can handle the loads that occur, the requirement of operational security can be met. The interrelationships of the various friction states in the bearing are depicted in Figure 1 using the Stribeck curve.

The hydrodynamic operation of the bearing (fluid friction)

To minimize power losses, designers of bearings for reciprocating engines strive for a state of fluid friction. Related studies of the physical processes have been conducted by Reynolds, Sommerfeld, Gümbel and others.

Figure 2 shows the hydrodynamic operation of a bearing. The space between the shaft and the bearing is called the lubrication gap and is filled with lubricant. The rotating shaft pulls lubricant into the diminishing lubricant gap, which induces the pressure behavior in the lubricant film as depicted in Figure 2.

Due to the localized pressure at the edge of the bearing, the pressure profile forms in axial direction.

The external forces on the lubricant (load from the shaft, etc.) and the lubricant film pressure form a dynamic balance. If rotational speed, size and direction of the load are constant, as in the stationary case, a stable state of the shaft occurs, that means constant eccentricity e with respect to direction and size.

This excentricity determines the smallest lubricant film thickness h0, which designates the smallest space between the shaft and the bore. The center of the shaft shifts on variation of the influencing factors on the near semicircular curve, the Gümbel circle. At infinitely high rotational speed, the shaft center (MW) theoretically shifts to the bearing center (ML).

The minimum lubricant film thickness h0 depends on the dimensions, the rotational speed, the load of the shaft, and the viscosity of the lubricant as well as on bearing clearance. The lubricant film becomes thicker with declining load, rising lubricant viscosity and increasing rotational speed. Due to the interplay of multiple parameters such as load capacity, temperature rise due to increased shearing forces in the oil, reduction

of oil throughput and thus the cooling capacity, as well as reduced tolerance for balance, form and dimensional deviations, changes in bearing clearance ø cannot be formulated as a general rule.

The following serve as reference values for the lower clearance limits: for conrod bearings 0,6 ‰ of the shaft diameter (dW), for main bearings 0,75 ‰. The associated upper clearance limits result from the respective tolerances. If improvements in the bearing situation are to be achieved through changes in the bearing clearance, these need to be assessed on a case-by-case basis.

Engine bearings

Bearing locations and their design

Using the example of a typical four-stroke diesel engine, Figure 3 depicts the bearing locations.

Figure 3: Bearing locations in an engine

Due to the different functionality of the various bearing positions, different methods of bearing design and interpretation criteria are used. Figure 4 depicts the typical steps for determining the installation situation, the bearing parameters and the bearing type for various bearing locations.

Camshaft bearings, conrod small end bearings. Thrust bearings. Gear bearings, statically loaded bearings

 Figure 5 shows interpretation criteria used for the individual methods. It is important to note that this state of the art continues to advance and thereby brings improvements in methods.

Bearing interference fit and stresses

Pretensioning the bearing half-shells in an installed state provides for a good contact of the bearing back with the housing.

This contact is necessary to prevent the bearing shell from turning in the housing and to assure heat dissipation through the bearing shell to the housing.

The circumferential length of the bearing shell is larger by a factor of the crush height (2 x SN) than the base bore of the housing; upon installation this stretches the base bore while elastically reducing the circumferential length of the bearing.

The circumferential pressure in the bearing causes a radial holding pressure (pr) between the bearing back and the housing, which provides a friction hold of the bearing in the housing.

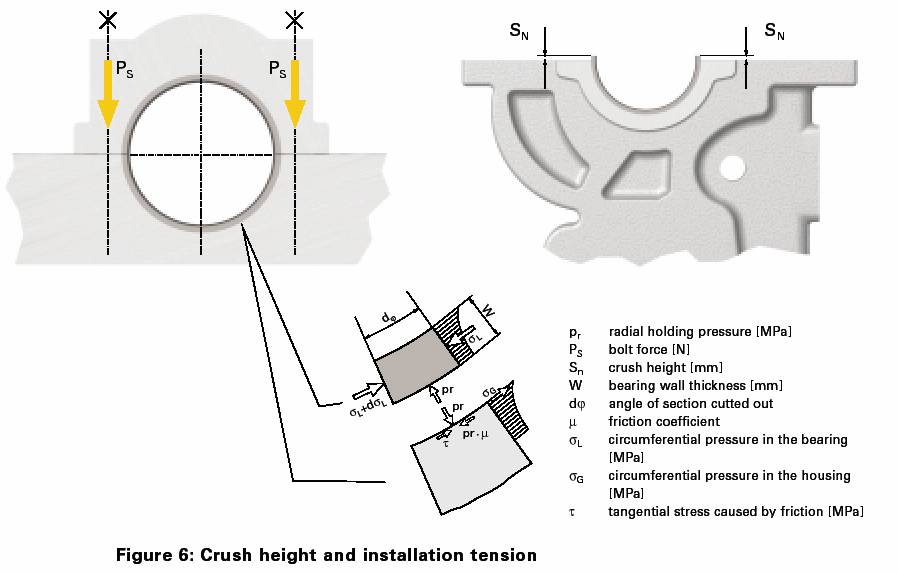
Figure 6: Crush height and installation tension

Load behavior

The bearing load in an engine for conrod and main bearings results from the interaction of gas and mass forces. Thus the direction and magnitude of the bearing force change continuously.

The forces on the engine that cause this nonstationary load are depicted in Figure 7.

Figure 7: Forces on an internal combustion engine

Figure 8 shows the typical force behavior for a conrod bearing, applied by magnitude and direction from the center. Due to the periodic nature of the four-stroke cycle, a closed curve results. On the curve the respective crankshaft position is given in degrees. Loads for stationarily loaded bearings can be computed according to the laws of statics.

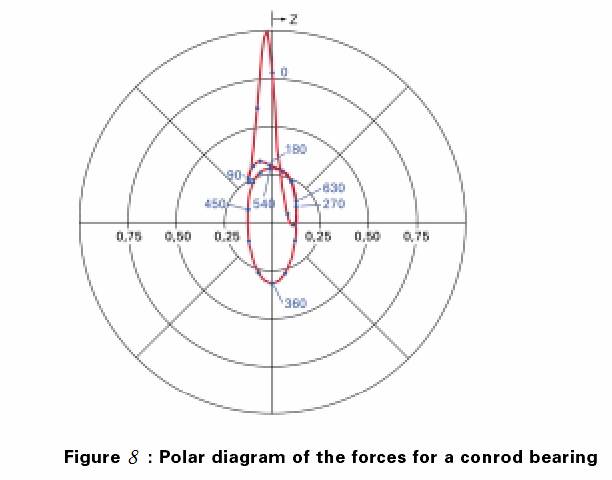
Figure 8: Polar diagram of the forces for a conrod bearing

Pin orbital path

For nonstationarily loaded bearings, the position and magnitude of the smallest lubricant film thickness changes due to the periodically changing forces. Once in every complete cycle, the resulting path of the pin center ensues; this is called the pin orbital path and can be computed with relatively little effort. In our case this method of computation is based on the Holland-Lang method with the Sommerfeld numbers according to Butenschön, and is used for the design of main, conrod- and camshaft bearings.

Figure 9 depicts a pin orbital path for a conrod big end bearing. The pin changes its position not only circumferentiallybut also radially. As the pin approaches the bearing surface, the pin displaces lubricant from the reduced gap. This displacement results in a very significantly increased load capacity of the lubricant film.

Typical values for the smallest lubricant film thickness (h0min) are 2–5 µm, which is a small percentage of bearing clearance, and thus also significantly less than the size of many particles transported by the lubricant.

Figure 9: Pin orbital diagram (pin path) for a conrod big end bearing, relative to bearing shell

Elastohydrodynamic lubricant film computation

Via the numeric solution of the Reynolds differential equation carried out on the present case, elastohydrodynamics affords the possibility of incorporating into the computation the respective rigidity of the bearing housing and special geometric characteristics of the bearing and the pin.

Figure 10 shows a typical housing model (part of conrod) with installed bearing shells as well as a development drawing of the bearing and pin.

Figure 10: Model of housing, bearing shells and pin for elastohydrodynamic lubricant film computation

With incorporation of the elastic deformation of the bearing environment, the lubricant film peak pressure declines in comparison to the computation of the orbital path. The smallest lubricant film thickness declines and often shifts to the edge of the bearing. The behavior of lubricant film pressure, clearance fill ratio and lubricant gap height can be studied over the complete cycle in relation to location and time. For the example of a conrod bearing with asymmetrical load applicaton, Figure 11 shows the three most important results – lubricant film pressure, clearance fill ratio (0.. empty, 1.. full) and lubricant gap height – shortly after top dead center ignition.

On the basis of the results above and the results and interpretation criteria in Figure 5, bearing optimization is possible, and an estimate of remaining service life can be added with the help of damage accumulation methods.

  Factors determining service life

In addition to functionality assessments by means of standard calculations, service life estimates have become increasingly important. Figure 12 summarizes the primary influencing factors.

How these individual factors influence the service life must be assessed for different engine applications (collective load) with consideration for the type of bearing used.